Plasmon Induced Heat Funneling from Au to Cu in the Bimetallic Au@Cu Core-Shell Nanoparticles

Metallic catalysts based on localized surface plasmon resonance (LSPR) in various compositions and structures have been widely studied [1-6]. There are two types of reaction mechanism for plasmonic nanostructures: photo-induced hot carriers (plasmonic photocatalysis) and light-excited phonons (photothermal catalysis) [7, 8]. Moreover, the hot carriers and phonon modes participate in the reaction together (plasmonic photothermal catalysis). The plasmonic photothermal catalysis has the advantages of plasmonic photocatalysis and photothermal catalysis. The excited hot electrons can directly participate in the reaction and the phonon modes can promote the mass transfer and reaction rate.

In addition to the monometallic catalyst, there are many researches focusing on designing bimetallic nanostructures (involving Au, Ag, Pt, Pd, Cu, and so on) to optimize catalytic activity and selectivity [3, 9-17]. The bimetallic nanostructures that mix a plasmonic metal with a transition metal in the form of the core-shell nanoparticles are more promising to promote catalytic performance. Usually they have a plasmonic core with a low imaginary dielectric function and a metal shell with chemically active site [4]. Due to the different free carrier density and effective mass in the two materials, the interfacial contact of bimetallic nanoparticles not only provides efficient energy flowing channels [4, 10] but also changes the carrier lifetimes [10].

The photoexcitation dynamics of the monometallic nanostructures has been already relatively clear. Metallic nanostructures have two kinds of temperatures after the LSPR excitation: electron temperature (T_e) and lattice temperature (T_l), namely, the two-temperature model (TTM) [18]. It involves electron heat capacity and lattice heat capacity. There are three dynamic processes in the monometallic nanostructures, as shown in FIG. S1(b) in Supplementary materials (SM) [19, 20]: (i) thermalization of non-equilibrium electrons by electron-electron scattering process (hundred of femtoseconds), (ii) heat transfer to the lattice through electron-phonon coupling process (a few picoseconds), (iii) heat transfer to the environment through phonon-phonon scattering process (hundreds of picoseconds). Different metals have different electron and lattice heat capacities [21], so the hot electron and phonon dynamics of the bimetallic nanostructures would be more complicated. Although there have been some studies about Au@Pt, Au@Pd, Au@Ag, Ag@Pt, and Cu@Au bimetallic core-shell nanostructures [3, 4, 9-11, 22-27], it is still unclear that how the heat (hot electrons and phonons) transfers on the interface between two metals. And these hot electrons and phonons, as well as their transfer, are important factors in plasmonic catalytic reactions [1, 2, 6, 7, 28-32].

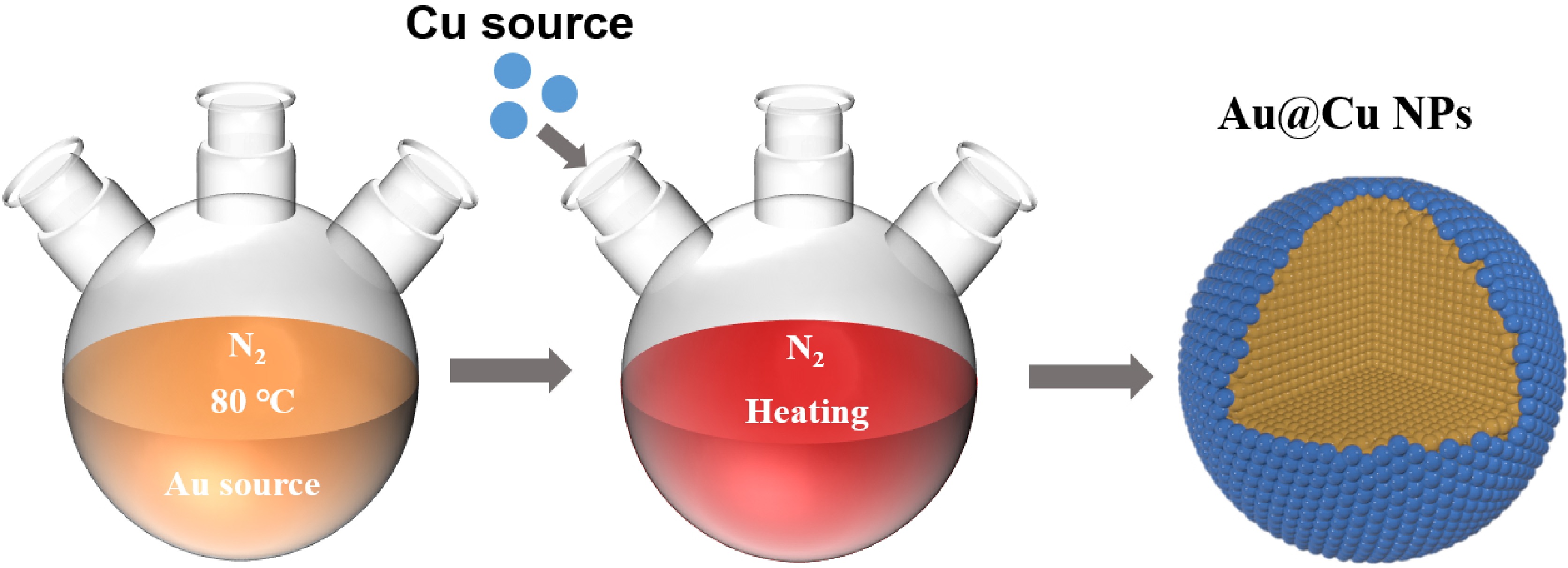
Herein, we have designed and synthesized the Au@Cu bimetallic nanoparticles (NPs) with Au as core and Cu as shell (Scheme 1, see Methods for details of synthesis). The Au@Cu NPs have a plasmonic core and an ultrathin catalytic shell, and the same sized monometallic Au NPs are also synthesized for comparison. By using transient absorption spectroscopy, we find that there are two plasmon induced heat funneling processes from Au core to Cu shell in the Au@Cu NPs besides the three dynamic processes of monometallic nanostructures. One is the electron temperature equilibrium (electron heat transfer) from Au core to Cu shell with equilibration time of ~560 fs. The other is the lattice temperature equilibrium (lattice heat transfer) from Au core to Cu shell with equilibration time of ~13 ps. They originate from the different heat capacities of Au core and Cu shell.

The following chemicals were purchased from Aldrich: Tetrachloroauric acid trihydrate (HAuCl₄·3H₂O, ≥99.9%), copper(I) chloride (CuCl, anhydrous, ≥99.99%, trace metals basis). The following chemicals were purchased from Sinopharm Group: 1-octadecene (ODE, technical grade, 90%), oleylamine (technical grade, 70%), toluene (analytical grade).

The Au nanoparticles (NPs) were synthesized by means of oil phase atmosphere according to the previous literature [10]. The reaction was carried out in a double row tube. The HAuCl₄ (106 mg) was dissolved in a mixture of 10 mL oleylamine and 10 mL ODE in 50 mL three neck flask. The mixed liquid was stirred at 500 r/min for 20 min under N₂ atmosphere. Then it was heated to 60 °C and continued to be stirred under N₂ atmosphere. The reaction was completed when the color of the solution varied from pale yellow to burgundy.

The synthesis of Au@Cu NPs with Au as core and Cu as shell is similar to previously reported Cu@Au bimetallic nanoparticles with Cu as core and Au as shell, and Au@Cu bimetallic nanorods with Au core and Cu shell [11, 33]. Anhydrous CuCl (99 mg, 1 mmol) was dissolved in a mixture of 5 mL oleylamine and 5 mL ODE in a 50 mL three neck flask under N₂ atmosphere and 80 °C. Then the mixture was injected into the Au NPs solution that was prepared following the steps above. The reaction was vacuumized under 80 °C for 30 min by using a standard Schlenk line technique. Then the flask was refilled with N₂. The reaction was heated to 100 °C. After 1 h, the solution was cooled down rapidly to room temperature. Note that the Au@Cu NPs were prepared by a modified seed-mediated approach. In this two-step synthesis method, the Au NPs were first prepared as seeds and then mixed with the copper salt precursor (Scheme 1). The color of the prepared Au NPs is burgundy red, which turns to dark red after successfully wrapping of Cu (see FIG. S2 in SM).

The steady-state UV-visible absorption spectra were measured by a U-3900 (Hitachi, Japan) spectrometer. The transmission electron microscope (Talos F200S type field emission, acceleration voltage of 200 kV) was used to observe the morphology and composition of the samples. The sample was dropped on the molybdenum support film to exclude the influence of Cu element on the carbon support film.

Femtosecond transient absorption measurement was performed by using an ultrafast transient absorption spectrometer (Harpia-TA, Light Conversion) that has been reported in our previous works [34, 35]. The femtosecond pulse produced by the amplified femtosecond Ti:sapphire laser (40 fs, 1 kHz, Coherent Astrella) has a central wavelength of 800 nm. The pulse of 800 nm was split into two beams as pump and probe pulses. The pump light was generated by an optical parametric amplifier (TOPAS-C, Coherent) with a wavelength of 400 nm. The probe was a white continuum light generated by focusing the femtosecond pulse on a CaF₂ plate. The polarization of pump light was magic angle relative to the probe light.

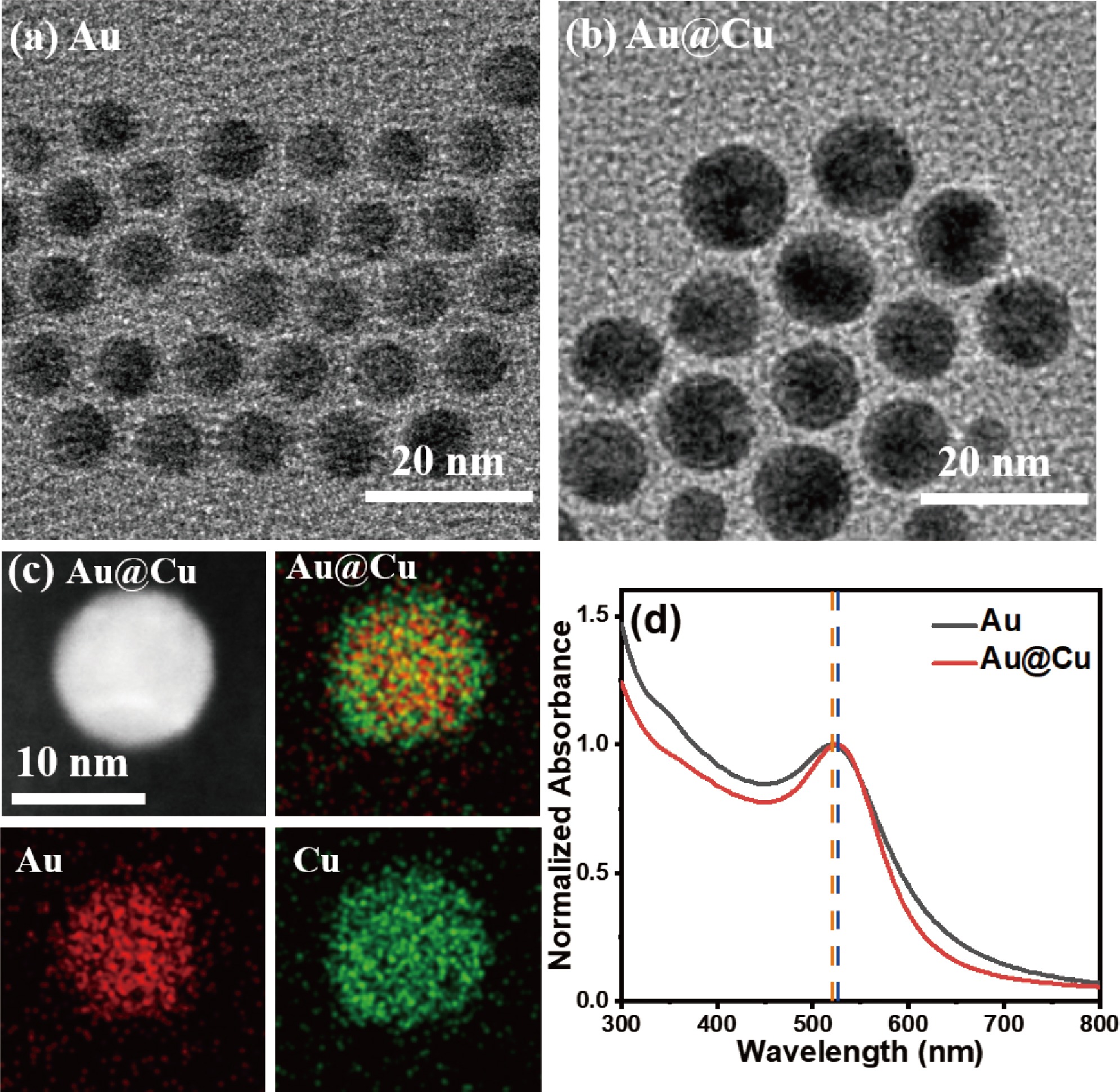
FIG. 1(a, b) shows the transmission electron microscopy (TEM) images of Au NPs and Au@Cu NPs. The Au NPs have uniform size of ~8 nm in diameter. The diameter of Au@Cu NPs has increased to ~11 nm. The larger size of Au@Cu NPs indicates the successful growth of copper on the surface of gold core which has a diameter of ~8 nm. According to the estimation method in literature [4], the copper coating should be more than five atomic layers thick. The high angle annular dark field scanning TEM (HAADF-STEM) and the energy dispersive X-ray (EDX) mapping analysis reveal the distribution of Au and Cu elements in the Au@Cu NPs as shown in FIG. 1(c). And the EDX line scan profiles of the Au@Cu NPs are also shown in FIG. S3 (SM). The Au@Cu core-shell nanoparticle is spherical. The Au core is spherical, so the EDX line-scan profile of Au element should have a shape of high center and both low sides. The Cu shell covers the whole surface of the Au sphere and should be a hollow sphere. The thickness of Cu shell is very thin (~1.5 nm), so the EDX line-scan profile of Cu element should be nearly constant throughout the structure. And the intensity of Cu should be higher than that of Au at the edge. Thus the EDX data have confirmed that the Au@Cu nanoparticles have the core-shell structure, similar to the reported CuS@ZnS core-shell nanoparticles [36]. Furthermore, the Au@Cu core-shell NPs with Au core and Cu shell have been synthesized on reduced graphene oxide substrate through a seed-mediated approach, which proves that copper can grow on gold cores [37].

The UV-Vis absorption spectra of Au NPs and Au@Cu NPs dispersed in toluene are shown in FIG. 1(d). The Au NPs and Au@Cu NPs have similar spectral features. The absorption spectrum of Au NPs reveals a well-known LSPR band centered at 535 nm. The LSPR band red-shifts ~5 nm for Au@Cu NPs compared with Au NPs. The LSPR band of pure Cu NPs is slightly redder than that of pure Au NPs [38, 39], so it seems that the LSPR of Cu shell in the Au@Cu NPs is also excited.

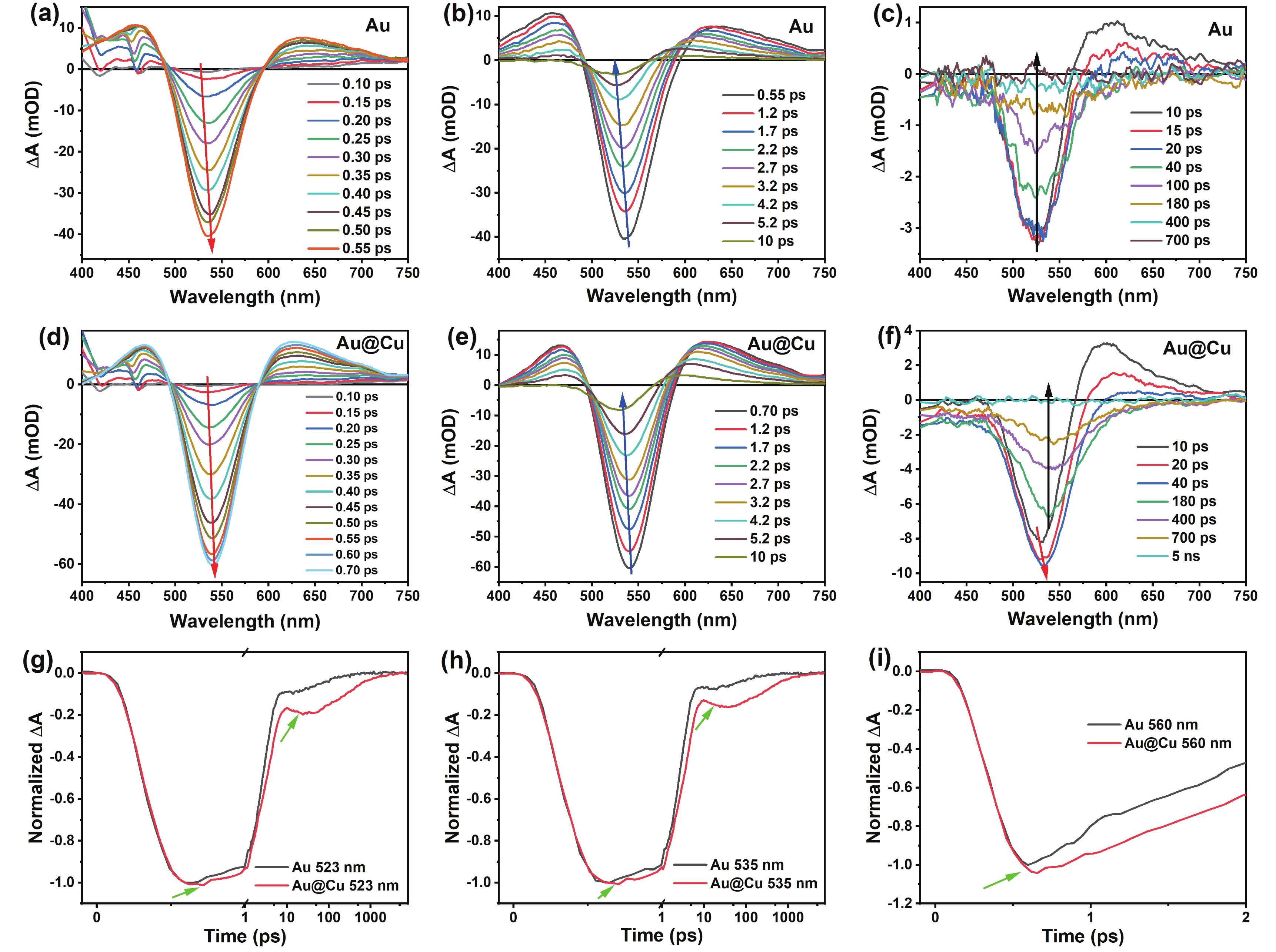
In the transient absorption (TA) measurement, the pump wavelength was chosen at 400 nm (3.1 eV) to induce interband transition (as shown in FIG. S1(a) (SM), ≥ 2.4 eV for gold or ≥ 2.21 eV for copper [40, 41]). The evolutions of TA spectra of Au NPs with different delay time are displayed in FIG. 2(a–c). The TA spectrum of Au NPs has a negative bleach peak centered at 535 nm (the Au LSPR band) and two positive bands on both sides of the bleach peak (caused by the LSPR peak broadening with increasing electron temperature [42]). The intense positive signal appearing at 400–450 nm and the hump at 455 nm before 0.4 ps are caused by the toluene solvent (see FIG. S4 in SM for the solvent only data).

At the first stage, the bleaching signal of the LSPR band has reached its maximum intensity within 0.55 ps as shown in FIG. 2(a) (IRF = 92 fs). After LSPR excitation, the electron temperature is developed by the electron-electron scattering process (electron thermalization) [19]. Due to the increase of electron temperature, the TA signal rises and appears redshifted as indicated by the red arrow in FIG. 2(a). Then the bleaching signal decreases rapidly, and it is blue-shifting with decay time of 0.55–10 ps due to electron cooling as shown in FIG. 2(b). The electron temperature decreases because of electron-phonon coupling, which leads to shorter LSPR wavelength [43]. After 10 ps, the TA signal decays slowly to none because of the lattice cooling process (phonon-phonon scattering [26, 44]) as shown in FIG. 2(c). The TA dynamics curves of Au NPs at selective probe wavelengths are also shown in FIG. 2(g–i). There are three distinct components: one rising process is the electron-electron (e-e) scattering, two decay processes are the electron-phonon (e-ph) coupling and the lattice cooling, respectively. The exponential fitting of the dynamics gives the equilibration times for electron-electron scattering of ~140 fs, the electron-phonon coupling of ~2.2 ps, and the lattice cooling of ~150 ps (see FIG. 3 and Table I for details, note that they are not the scattering or coupling constant), which agree well with previous reports [19, 45-47].

Compared with Au NPs, the negative bleach peak (the LSPR band) of Au@Cu NPs is red-shifting ~5 nm, which corresponds to the steady-state absorption spectra. As shown in FIG. 2(d–f), the evolution of TA spectra with time delay of Au@Cu NPs is different from that of Au NPs in the initial 700 fs and also the tens of picoseconds.

At the first stage (FIG. 2(d)), the bleaching signal of the Au@Cu NPs exhibits a rising and red-shifting over 0.7 ps, which is longer than that of Au NPs. This can be confirmed by the comparison of dynamics as shown in FIG. 2(g–i), note that the dynamics curves have been normalized to make Au and Au@Cu have the overlapped rising edge. This indicates that the electron thermalization process of Au@Cu NPs is slower than that of Au NPs. There could be some reasons causing the slower electron thermalization: one is the electron-electron scattering of copper, but the e-e scattering process in Cu NPs should be faster than that in Au NPs under the same excitation conditions [48]. Another is the size effect of e-e scattering of gold core, but the gold core of Au@Cu NPs has the same size as the pure Au NPs, then the effect of size can be ruled out. So we think that the extended electron thermalization in Au@Cu NPs is the contribution from the interaction between the Au core and Cu shell. In other words, in addition to the electron-electron scattering, there should be one more process which is called the electron temperature equilibrium between Au core and Cu shell (the detailed assignment will be discussed in the next section).

In the time range of 0.7−10 ps, the bleaching signal of Au@Cu NPs decays and blue-shifts due to the electron-phonon coupling (FIG. 2(e)), which is the same as Au NPs. But from 10 ps to 40 ps, different from the Au NPs, the bleaching signal of Au@Cu NPs rises again and is accompanied by red shifting as shown in FIG. 2(f). This is quite evident by comparison of dynamics as shown in FIG. 2 (g) and (h). So there should be another additional process after the electron-phonon coupling. We call it the lattice temperature equilibrium between Au core and Cu shell (the detailed assignment will be discussed in the next section). Finally, the TA signal of Au@Cu NPs decays to none in a few nanoseconds because of the lattice cooling process which is slower than that of Au NPs.

To sum up, there are five distinguishable dynamic processes for Au@Cu NPs. The first, second, and fourth are TA signal rising process. The third and fifth are TA signal decaying process. It needs a five-exponential function to fit the TA dynamics. As shown in FIG. 3 and Table I, the exponential fitting of the dynamics of Au@Cu NPs gives the equilibration times for electron-electron scattering of ~136 fs, the electron temperature equilibrium of ~560 fs, the electron-phonon coupling of ~2.4 ps, the lattice temperature equilibrium of ~13 ps, and the lattice cooling of ~420 ps.

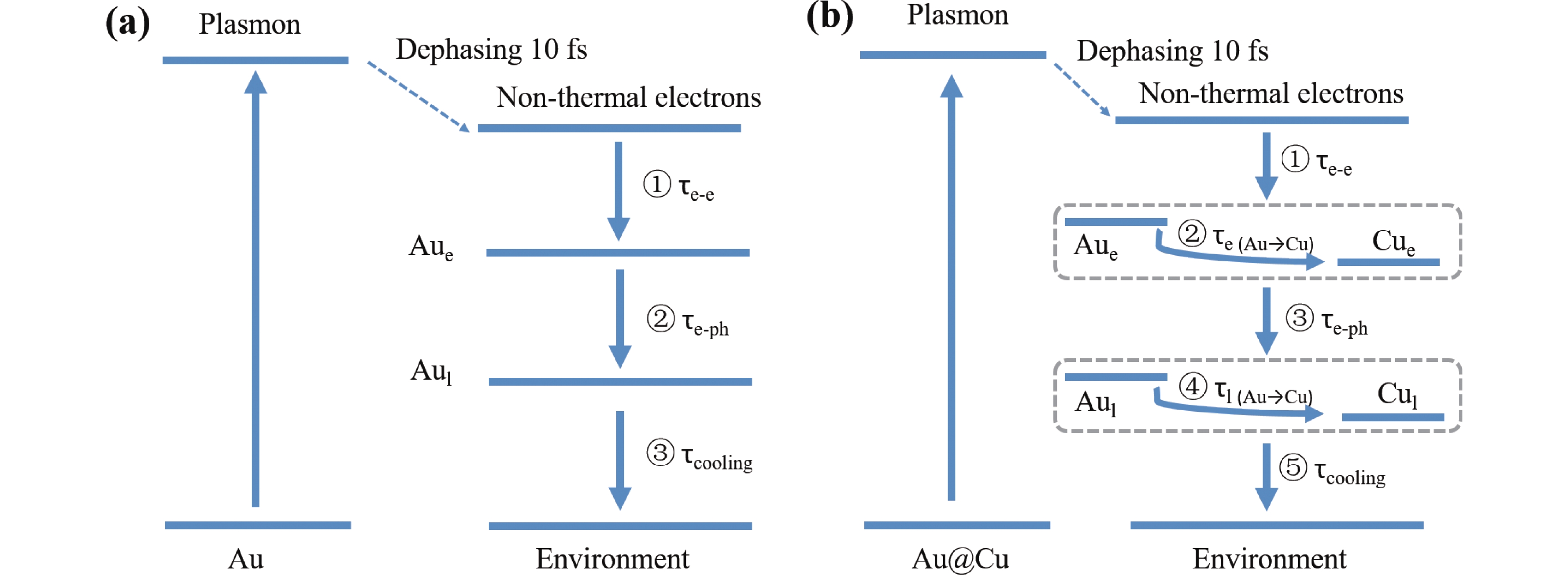
For a monometallic nanostructure, the two-temperature model (TTM) has been used to describe the photoexcitation dynamics [19, 49-53], in which electron temperature T_e exchanges energy with the lattice temperature T_l and T_l exchanges energy with the surroundings temperature T_s. Scheme 2(a) displays the dynamics processes of the monometallic Au NPs, which bases on the TTM [10, 19, 54, 55]. The TA signal changing is caused by the variation in electron temperature [46], in which the occupied states near the Fermi level have changed as shown in FIG. S1(b) (SM) [54]. When the electrons are excited by light, they develop electron temperature through electron-electron scattering process (collision between excited electrons and unexcited electrons). Due to the vastly different heat capacities of electron and lattice, the electron temperature is much higher than the lattice temperature [52, 54]. Then the electron temperature and lattice temperature reach an approximate equilibrium through the electron-phonon coupling process in which the TA signal decays a lot. The residual TA signal is caused by the heated (expanded) lattice, and it decays slowly because of the phonon-phonon scattering process with surroundings accompanied with lattice cooling (shrinking) [10, 56, 57]. So we have observed three dynamics processes for Au NPs as shown in the TA data.

For the bimetallic Au@Cu NPs, both of Au core and Cu shell can be excited because the copper coating is only five atomic layers thick (~1.5 nm). So the hot electrons should be generated in two parts: Au core and Cu shell. Both of the electron-phonon coupling constant and electron heat capacity of Cu are larger than those of Au according to the calculated results [21]. In general, a higher electron heat capacity induces to a relatively lower peak electronic temperature after the LSPR excitation [58]. Therefore, Cu shell should have a lower electron temperature than Au core after the respective electron-electron scattering. The temperature gradient between the Au electron and the Cu electron would drive heat flow from hot electron of Au core to hot electron of the Cu shell by electrons collision. When the temperature of the entire system approaches equilibrium, the rising process of TA beaching signal (indicating the electron temperature) would slow down. So there should be an electron temperature equilibrium process in 700 fs in Au@Cu NPs (see FIG. 2(d)). And it is slower than the electron-electron scattering in each metal because of the limited interface between two metals. Similar phenomenon has been demonstrated in Au@Pt bimetallic nanostructures [4, 10, 59].

Then the heat of electron transfers to the lattice through the electron-phonon coupling process in each metal, respectively. Similar to electron, a higher lattice heat capacity induces to a relatively lower lattice temperature [21, 54]. The higher lattice heat capacity of Cu than that of Au will lead to the lower lattice temperature of Cu shell than Au core after the respective electron-phonon coupling. The temperature gradient between the Au lattice and the Cu lattice would drive heat transfer from lattice of Au core to lattice of the Cu shell by phonons scattering. Therefore, the amplitude of TA bleaching rises with the increasing of the temperature of the Cu lattice (note that the hot electron and heated lattice of Cu nanostructure have TA signal too [38]). When the temperature of the entire system approaches equilibrium, the rising process of TA beaching signal (indicating the lattice temperature) would slow down. So there should be a lattice temperature equilibrium process from Au core to Cu shell in 40 ps in Au@Cu NPs (see FIG. 2(f)).

After the lattice temperature equilibrium, the heat in Cu lattice transfers to the surroundings (solvent) by the phonon-phonon scattering process accompanied with lattice cooling (shrinking). The thermal resistance of Cu shell is larger than that of Au core [1], so the equilibration time of lattice cooling is longer in Au@Cu NPs than Au NPs (see τ₅ in Table I).

Summing up the above, if considering the dynamics in Au core and Cu shell respectively, there should be electron-electron scattering in Au core, electron temperature equilibrium from Au core to Cu shell, electron-phonon coupling in Au core, lattice temperature equilibrium from Au core to Cu shell, electron-electron scattering in Cu shell, electron-phonon coupling in Cu shell, phonon-phonon scattering between Cu shell and solvent. But some equilibration times are very close to each other and hard to distinguish in the TA data. So we can treat Au core and Cu shell as a system, combining the electron-electron scattering in two metals and also the electron-phonon coupling in two metals. Thus there are only five processes in the Au@Cu system. As shown in Scheme 2(b), they are electron-electron scattering, electron temperature equilibrium, electron-phonon coupling, lattice temperature equilibrium, and lattice cooling. And the first, second and fourth processes lead to the rising of TA signal. The third and fifth processes lead to the decaying of TA signal. It matches the result of our TA experiment well. So it is reasonable to use the five processes scheme to fit the TA dynamics (FIG. 3 and Table I).

We have also measured the transient absorption spectra of Au NPs and Au@Cu NPs under different pump fluence (133.75 µJ/cm², 400 nm) to examine the hot electron and phonon dynamics. As shown in FIG. S5, S6 and Table S1 (SM), similar dynamic processes are observed but with different equilibration times. The higher pump fluence corresponds to slower electron-phonon coupling (τ₃). The reason for it is that higher excitation density could lead to higher initial electron temperature [19, 60], The difference between the fitted τ₁ or τ₂ of two pump fluence is only tens of fs. Considering our IRF is 92 fs, it is hard to confirm the influence of pump fluence to electron-electron scattering and electron temperature equilibrium processes. When the heat has transferred to the lattice of Au and Cu, the lattice temperature is already quite low regardless of the pump fluence, so lattice temperature equilibrium and lattice cooling are not sensitive to the pump fluence. The pump fluence dependence on the dynamics is not conflict with our assignment for Au@Cu NPs. It gives some evidence to the reasonability of the dynamics processes described in Scheme 2(b).

In summary, as shown in FIG. 4, the dynamic processes following LSPR excitation of bimetallic Au@Cu NPs are significantly different from that of monometallic Au NPs. There are two more processes in Au@Cu NPs due to the different heat capacities of Au core and Cu shell. One is the electron temperature equilibrium from Au core to Cu shell with equilibration time of ~560 fs. The other is the lattice temperature equilibrium between Au core to Cu shell with equilibration time of ~13 ps. This plasmon induced heat funneling may be universal in similar bimetallic nanostructures, so our finding could contribute to further understand the catalytic mechanism of bimetallic plasmonic photothermal catalysis. Core shell nanoparticles with plasmonic core and ultrathin catalytic shell will be promising for the development of highly efficient plasmon-driven catalysts.

Supplementary materials: Cartoon of the band structure and dynamics, and additional TA data and fitting results of Au and Au@Cu NPs are shown.